[이코테] 바닥 공사 - Bottom up 방식
2022. 3. 7. 20:18ㆍ알고리즘/DP
문제 :
가로의 길이가 N, 세로의 길이가 2인 직사각형 형태의 얇은 바닥이 있음.
이 바닥을 1*2, 2*1, 2*2 덮개를 사용해 채우고자 함.
바닥을 채우는 모든 경우의 수를 구하는 프로그램을 작성하기.
입력 조건 : 첫째 줄에 N이 주어짐.
출력 조건 : 첫째 줄에 2*N 크기의 바닥을 채우는 방법의 수를 796,796으로 나눈 나머지를 출력.
[풀이]
동적 프로그래밍으로 푸는 만큼 이전에 계산했던 부분을 다시 계산하지 않는 것이 핵심인 거 같다.
일종의 점화식으로 풀었다.
- 만약 내가 N번째를 구하려고 한다면 N-1 번째에서 미리 계산되어 있던 것을 배열에 집어넣고
N-1번째를 활용해서 N번째를 구한다.
- 더불어 여기서 알게 된 것은 무조건 N-1번째만 활용하려고 하지 않는다는 것이다. N-1번째만 활용해야 하는 생각에 문제가 너무 안풀렸었다.
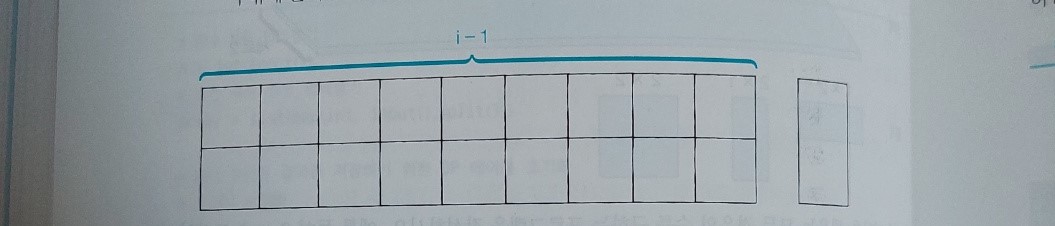
가령 이러한 경우는 N-1번째의 수에서 2*1 덮개를 추가하는 형태 하나이기 때문에 N-1를 그대로 더하면 된다.
하지만 1*2 덮개 2개와 2*2덮개 1개를 추가하는 경우에는 다음과 같다.

이렇게 두 개를 생각해야하기 때문에 식을 세울 때 무조건 n-1만 써야한다는 생각에서 벗어난 거 같다.
그리하여 쉽게 설명하자면 n의 값은 n-1번째와 n-2를 두번 더한 값이다.
즉, arr[n] = arr[n-1] + arr[n-2] + arr[n-2] 인 것이다.
이를 구현한 자바 코드는 다음과 같다.
import java.util.Scanner;
public class floorConstruction {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// n 입력받음.
int n = sc.nextInt();
// 저장할 수 있는 배열 선언 및 초기화
int dp[] = new int[n+1];
// 1과 2의 값 넣기
dp[1] = 1;
dp[2] = 3;
// Bottom up 진행방식
for(int i=3; i<=n; i++) {
dp[i] = (dp[i-1] + 2*dp[i-2])%796796 ;
}
// 값 출력
System.out.println(dp[n]);
}
}'알고리즘 > DP' 카테고리의 다른 글
| [이코테] 화성탐사 (0) | 2022.04.15 |
|---|---|
| [이코테] 동적 프로그래밍(Dynamic Programming) 정리 (0) | 2022.04.05 |
| [이코테] 구현 - 뱀 (0) | 2022.03.25 |
| [이코테] 경쟁적 전염 (0) | 2022.03.25 |