2022. 4. 8. 16:42ㆍ알고리즘/그래프
[정의] 가장 짧은 경로를 찾는 알고리즘
- 다익스트라 알고리즘
특정한 노드에 출발하여 다른 모든 노드로 가는 최단 경로 계산
그리디 알고리즘으로 분류 (매 상황에 가장 적은 노드 선택)
시간 복잡도 O(N^2) -> 우선순위 큐 사용 O(NlogN) 줄임. 힙 연산.
원소를 모두 우선순위 큐에 넣었다가 모두 빼내는 연산과 유사. (ElogV : E는 간선, V는 노드)

방법
1. 출발노드 설정
2. 최단 거리 테이블 초기화
3. 방문하지 않은 노드 중 최단 거리가 가장 짧은 노드 선택
4. 해당 노드를 거쳐 다른 노드로 가는 비용 계산 -> 최단 거리 테이블 갱신
5. 3-4번 반복
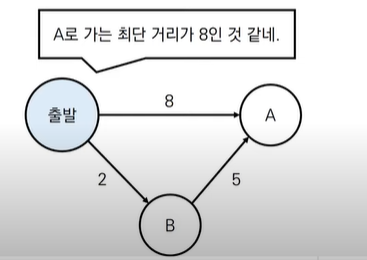
: 매 단계마다 노드를 순차적으로 탐색
< Java >
- boolean visited[] : 노드 방문 true/false
- int graph[][] : 연결되어 있는 노드에 대한 정보
- 클래스 Node 정의.
: 입력된 모든 노드를 graph 통해 받음. -> Node 클래스에 하나씩 짝으로 넣기(idx, dist) -> 시작점(start) 에 방문처리를 하면서 인접노드를 순회하며 기존에 있던 값에서 더하여 더 작다면 작은 값을 반영 -> visited에서 순회하여 간선이 작은 노드부터 방문 시작 (같다면 값이 작은 노드부터)
코드 구현
package codingTest;
import baekjoon.Array;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;
class Node {
// 이어지는 노드와 거리 저장.
private int idx;
private int dist;
public Node(int idx, int dist) {
this.idx = idx;
this.dist = dist;
}
public int getIdx() {
return this.idx;
}
public int getDist() {
return this.dist;
}
}
public class Dijkstra {
// 무한
public static final int INF = (int) 1e9;
// 노드 갯수
public static int n;
// 간선 갯수
public static int m;
// 시작 노드
public static int start;
// 간선 계산 배열
public static int d[] = new int[100001];
// 방문 노드
public static boolean visited[] = new boolean[100001];
// 간선과 값 저장 배열
public static ArrayList<ArrayList<Node>> graph = new ArrayList<ArrayList<Node>>();;
public static int getSmallestNode() {
int val = INF;
int num = 0;
// 방문 하지 않은 노드 중 가장 작은 노드 찾기
for (int i = 1; i <= n; i++) {
if(d[i] < val && !visited[i]) {
val = d[i];
num = i;
}
}
return num;
}
public static void dijkstra(int start) {
// 시작 노드 초기화
d[start] = 0;
visited[start] = true;
for (int i = 1; i <= d.length; i++) {
int idx = getSmallestNode();
visited[idx] = true;
for (int j = 0; j < graph.get(i).size(); j++) {
// Array 에 저장되어 있는 연결 노드 간선을 꺼냄.
int cost = d[idx] + graph.get(idx).get(j).getDist();
// 저장되어 있는 값보다 게산 값이 더 작다면?
if(cost < d[graph.get(idx).get(j).getIdx()]) {
d[graph.get(idx).get(j).getIdx()] = cost;
}
}
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
start = sc.nextInt();
// 그래프 초기화
for (int i = 0; i < n; i++) {
graph.add(new ArrayList<Node>());
}
// graph에 저장
for (int i = 0; i < m; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
graph.get(a).add(new Node(b, c));
}
// 값 저장하는 그래프 무한으로 초기화
Arrays.fill(d, INF);
dijkstra(start);
}
}- 플로이드 워셜 알고리즘
모든 노드에서 다른 노드까지의 최단 경로를 모두 계산
매 단계마다 방문하지 않은 노드 탐색하지 않음. : 2차원 테이블에 최단거리 정보 저장.
다이나믹 프로그래밍 유형.
총 시간 복잡도는 O(N^3) : 2차원 배열 탐색 O(N^2) + 노드의 수(N)만큼 단계를 반복
방법
특정한 노드 k를 거쳐가는 경우 확인. : a에서 b로 가는 최단거리보다 a에서 k를 거쳐 b까지 가는데에 거리가 더 짧은지 검사.
점화식은 다음과 같음.

초기 상태 (세로 줄은 출발하는 노드, 가로 줄은 도착하는 노드)


< Java >
- int graph[][] 노드의 정보가 담긴 그래프
: 3중첩 for문을 활용하여 a와 b 노드 사이에 k를 지나는 노드 중에서 작은 것을 선택하여 반영
코드 구현
package codingTest;
import java.util.ArrayList;
import java.util.Scanner;
public class Floyd {
// 무한
public static int INF = (int) 1e9;
public static int n;
public static int m;
public static void floyd(int graph[][]) {
//알고리즘을 통해 그래프를 정렬.
int len = graph.length;
for (int i = 1; i < len; i++) {
for (int j = 1; j < len; j++) {
for (int k = 1; k < len; k++) {
graph[i][j] = Math.min(graph[i][j], graph[i][k] + graph[k][j]);
}
}
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// 노드의 갯수
n = sc.nextInt();
// 간선의 갯수
m = sc.nextInt();
// 그래프 선언
int graph[][] = new int[n+1][n+1];
// 무한으로 초기화 & 노드 자신은 0으로 표현
for (int i = 1; i < n+1; i++) {
for (int j = 1; j < n+1; j++) {
if(i==j) {
graph[i][j] = 0;
} else {
graph[i][j] = INF;
}
}
}
// 간선의 갯수만큼 graph[][]에 값을 넣음.
for (int i = 0; i < m; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
graph[a][b] = c;
}
floyd(graph);
}
}
'알고리즘 > 그래프' 카테고리의 다른 글
| [백준] 유기농 배추 (2) (0) | 2022.04.23 |
|---|---|
| [백준] 유기농 배추 (1) (0) | 2022.04.20 |
| [이코테] 탑승구 (0) | 2022.04.18 |
| [이코테] 탐색 알고리즘 DFS/BFS (0) | 2022.03.21 |
| [그래프] DFS : 배열로 구현 (0) | 2022.01.24 |